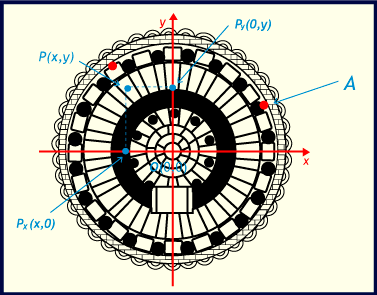
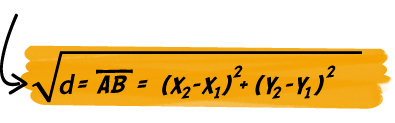En esta actividad tú objetivo será construir una expresión matemática que permita desencantar el tesoro escondido en el templo de Ethos pero ahora usando un sistema de coordenadas cartesianas.
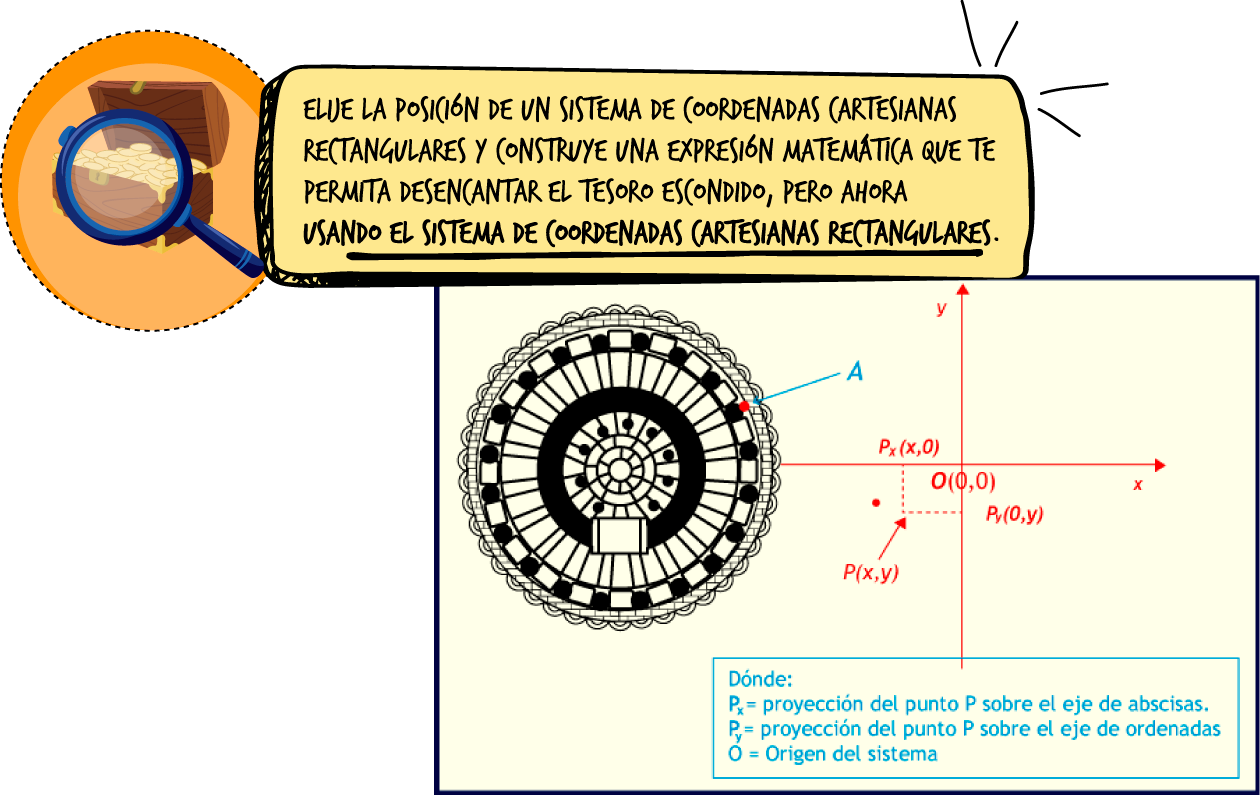

La mejor posición del sistema, para indicar la posición de los puntos que están al borde del templo, es cuando el origen O coincide con
Con base en lo que observas en la imagen del templo de Ethos, Responde la consigna que se te presenta. Haz click sobre la imagen para ampliarla.

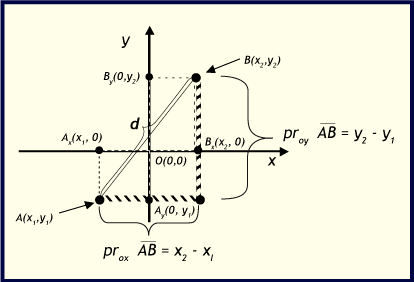
Revisa la siguiente información. Haz click sobre la imagen para ampliarla.
El cálculo de la distancia entre dos puntos conocidas sus coordenadas es un problema elemental de la geometría analítica y se apoya en otro problema elemental: el calculo de la proyección de un segmento orientado sobre un eje.
Así: Dados los Puntos y . Entonces
a) La proyección del segmento sobre el eje de las abcisas es:
b) La proyección del segmento sobre el eje de ordenadas es:
Y la distancia se calcula aplicando el teorema de Pitágoras en el triángulo rectángulo ABC.

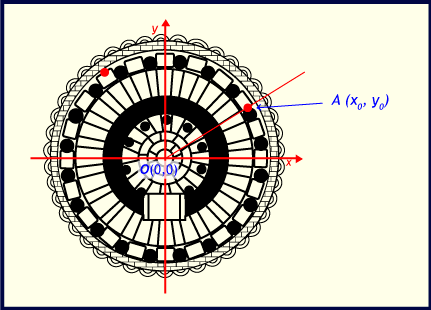
Con base en la información que se te presenta y la imagen, responde la pregunta planteada.
Si la expresión matemática que define cualesquiera de los puntos que están en la periferia del templo de Ethos es:
La coordenada del punto C es:
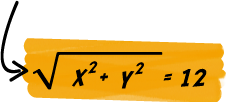
Restringiéndonos a los observables del plano y tomando como unidades de medida:
 (u) el radio de la circunferencia más pequeña, como la unidad de medida de las longitudes;
(u) el radio de la circunferencia más pequeña, como la unidad de medida de las longitudes; (a) el arco de la circunferencia más externa, subtendido por el ángulo central de la circunferencia como unidad de medida de los ángulos;
(a) el arco de la circunferencia más externa, subtendido por el ángulo central de la circunferencia como unidad de medida de los ángulos;
Para resolver la pregunta anterior usted tuvo que movilizar eficazmente los siguientes recursos:

- Leer y analizar las proposiciones de los tres distractores para concluir que: el distractor a) proporciona valores aproximados, de las proyecciones del punto A sobre los ejes, obtenidos por la simple inspección visual lo cual no parece ofrecer garantía suficiente sobre los valores.
- El distractor b) expresa los valores como proyección sobre los ejes de coordenadas del segmento lo cual es correcto, según la definición de coordenadas y como se muestra en la gráfica
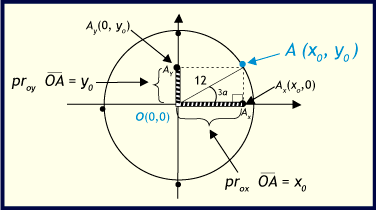
- Para calcular el valor de las proyecciones , es necesario considerar el triángulo rectángulo y aplicar las funciones seno y coseno al ángulo θ en el vértice O.
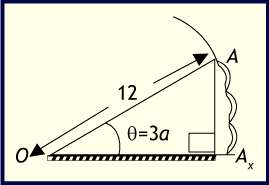
Así
, y ,
(I)
Recordemos que el ángulo se mide con relación a la unidad de medida a que resulta de dividir la circunferencia en 36 partes (arcos) iguales. Es decir θ= 3a.
- Para calcular los valores del seno y el coseno del ángulo θ= 3a debemos expresarlo en unidades estándar -grados o radianes- y elegimos los grados
donde L es la longitud de una circunferencia cualquiera.
Y de acuerdo a la manera como se definió el patrón de medida a se tiene que:
Donde L es la longitud de la circunferencia más externa -se dividió en 36 partes (arcos) iguales.
Así, despejando L e igualando las dos expresiones se tiene:
, entonces,
Por tanto
- Se calcula el seno y el coseno de
Y se reemplazan en (I) y se obtienen las coordenadas de A: El par ordenado
(10.4, 6)
Diseñamos esta situación de tal manera que hiciera necesario que realizaras las siguientes acciones
- Elegir un sistema de referencia -origen y ejes-, para ubicar puntos del plano.
- Representar puntos del plano, usando un método para hacer corresponder cada punto con un par de números -un punto en el plano se determina con dos números- empleando un patrón de medida conveniente y definiendo una manera de obtener tales números.
- Elegir y Comparar patrones de medida, estableciendo equivalencias entre las unidades de medida elegidas y las unidades estándar para realizar conversiones
- Representar, con una expresión matemática, la posición de un conjunto de puntos del plano que estaban sometidos a la condición de pertenecer al borde de un templo circular.