Con base en la historieta de Simón, ahora tendrás la oportunidad de hallar la respuesta a la pregunta: ¿Qué cantidad de tazas de moras, azúcar y harina debes agregar para ayudar a simón a hacer el pastel de mora?
Ajusta las porciones de azúcar, mora y harina usando los respectivos botones sobre cada producto (azul, rojo, fucsia) y enciende el horno llevando la palanca de OFF a ON.
Con base en lo que has desarrollado con ayuda de la aplicación, responde la siguiente pregunta
¿Cuál de los siguientes esquemas ilustra mejor el procedimiento que usaste para encontrar las tazas de mora, harina y azúcar?
Lo anterior permite concluir que las tazas de mora no pueden ser 5 porque no se cumple una de las condicione de la receta del pastel de mora. Este “fracaso” es la base para encontrar la respuesta correcta –aprendemos de los errores. Claramente hay que aumentar o disminuir el número de tasas de mora. Se elige una opción razonable y se continúa el proceso hasta obtener el resultado que se ajusta a las tres condiciones.
SI NO LO HICISTE ASÍ, PUEDES INTENTARLO
1 paso: Se despeja H de las dos primeras ecuaciones y se igualan
2 paso: Repitiendo el paso 1, despejamos A
3 paso: igualamos y despejamos M
Si ajustamos las tazas de manera aleatoria, las posibilidades son muchas, observe que cada cantidad de tazas varia de 1 a 10, así tenemos para la primera opción, que es tazas de azúcar 10 posibilidades, para la segunda opción que es tazas de mora, 10 posibilidades, hasta este punto las combinaciones serian 10x10=100, pero falta la tercera opción que son tazas de harina, es decir las posibilidades si consideramos ensayo y error sin ningún tipo de discernimiento serian 10x10x10=1000.
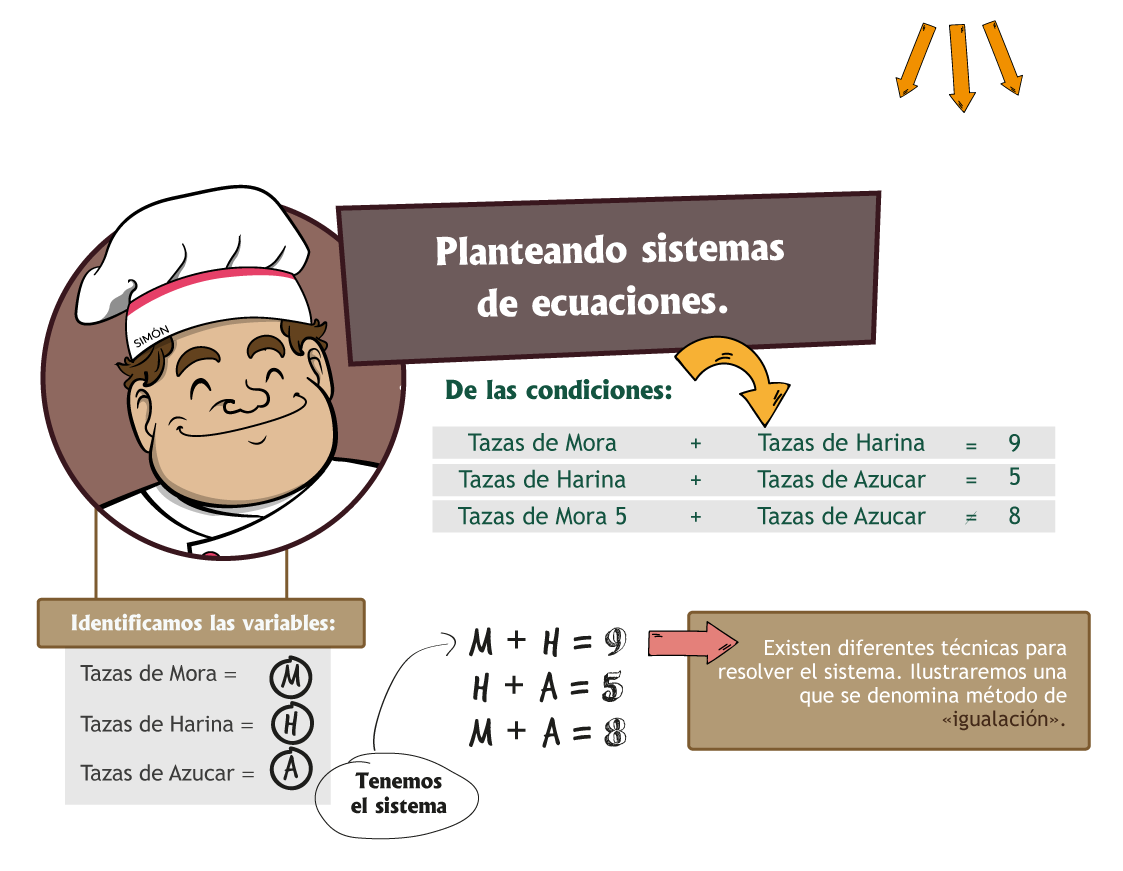
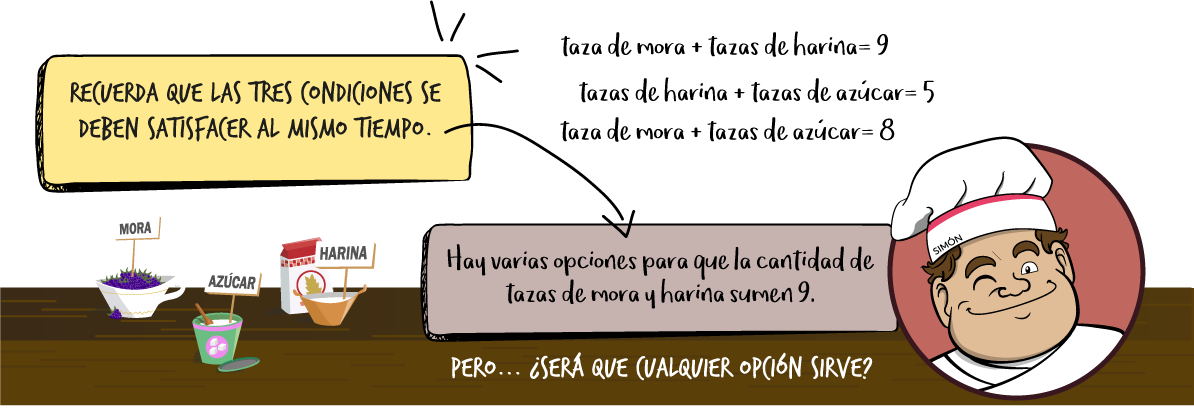
A este procedimiento se denomina «discernimiento». El discernimiento es un acto de pensamiento fundamental en la resolución de problemas no solo matemáticos, si no de la vida. Discernir es razonar con sentido y los matemáticos construyen formas de esquematizar estos discernimientos que se aplican a situaciones de la misma familia. En este caso se trata de escribir las condiciones por medio de ecuaciones así:
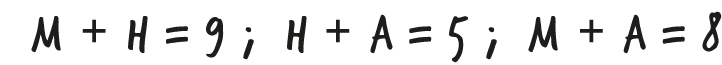
Como las incógnitas están relacionadas por las tres ecuaciones se denomina un sistema de ecuaciones. Y se acostumbra a escribir de la siguiente manera:
Para este ejemplo se utilizó el método de igualación, pero existen dos métodos más que son; sustitución y reducción.
Esperábamos que esta actividad te permitiera:
- Comprender y manipular información en distintos formatos: (lenguaje natural, algebraico, numérico e icónico)
- Establecer relaciones aditivas entre cantidades
- Diseñar estrategias y alternativas para la solución de problemas: establecer las relaciones aditivas entre las cantidades desconocidas
- Utilizar herramientas cuantitativas para solucionar problemas: encontrar las cantidades que satisfacen las relaciones por discernimiento usando la herramienta en la actividad 2 o resolviendo un sistema de ecuaciones de primer grado.
Se despeja una de las variables y se sustituye en la otra ecuación, despejando de (1) H= 9 – M, sustituyendo en (2), 9 – M + A = 5, despejando A, A = M - 4 , sustituyendo en (3), M + M – 4 = 8, de donde M = 6
El objetivo es cancelar variables, fijamos una variable a cancelar, en este caso H, multiplicando por -1 la ecuación (1), - M – H = -9, sumando esta ecuación a la ecuación (2) tenemos -M – H + H + A = -9 + 5, de donde -M + A = -4, multiplicando por -1 tenemos M – A = 4, sumando esta ecuación a la ecuación (3) M – A + M + A = 4 + 8, cancelando A y despejando M se llega a que M = 6